Предельное равновесие в точке и положение поверхностей скольжения. Расчётное сопротивление грунта

Давление Р от веса надземной части сооружения и собственного веса фундамента, воспринимаются основанием рассеивается в массиве грунта. Равнодействующую R передачи давления между частицами грунта можно разложить на две составляющие (см. схему): нормальные напряжения (σ) и касательные (τ). Нормальные напряжения σ – сжимают частицы грунта друг к другу и разрушить их практически не могут (частицы грунта – кварц, полевой шпат и т.д.)

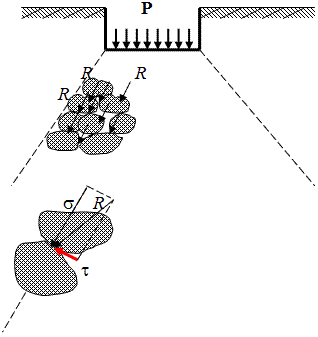
Схема рассеивания напряжений в массиве грунта под подошвой фундамента.

Для разрушения минеральных частиц грунта нормальными напряжениями необходимы величины σ_{разруш.} ≈ 2000 кг/см² ≈ 200 МПа, но таких напряжений под фундаментом практически не возникает. Следовательно, разрушение грунта может происходить только от действия сил τ. Под действиями данных сил частицы грунта смещаются относительно своих контактов, зерна попадают в поровое пространство, происходит процесс уплотнения грунта с возникновением в некоторых областях поверхностей скольжения (τ_пр).

τ_пр – предельное касательное напряжение или предельное сопротивление грунта сдвигу (определяется экспериментально в сдвиговом приборе с использованием теории Мора–Кулона).

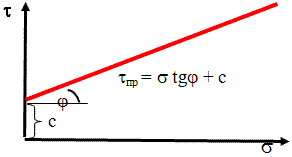
Графическое представление сопротивление грунта сдвигу по теории Мора-Кулона.

Как же происходит разрушение грунта? Для ответа на этот вопрос рассмотрим схему проведения испытаний образца грунта в приборе трехосного напряженного состояния или в стабилометре (правая схема на ниже приведенном рисунке). Цель испытаний – получить расчетные прочностные характеристики грунта в момент его предельного состояния, т.е. разрушения. Эти испытания имеют аналогию с одноосным разрушением образца материала, проводимого в лаборатории строительных материалов (левая схема на ниже приведенном рисунке). В том и другом случаях поверхность разрушения образца наклонена к горизонту под углом α.

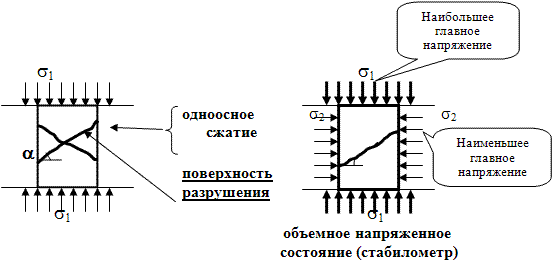
Различные схемы испытаний грунта в зависимости от его исходного состояния.

Для определения положения поверхности предельного состояния, вырежем из массива грунта призму с гранями параллельно главным нормальным напряжениям и рассмотрим условия ее равновесия.

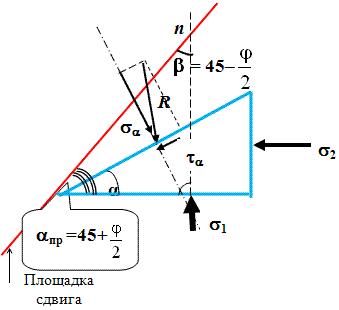
Схема работы призмы грунта с формированием поверхности скольжения (площадок сдвига) в момент предельного состояния.

Общее напряженное состояние грунта можно характеризовать кругом Мора.

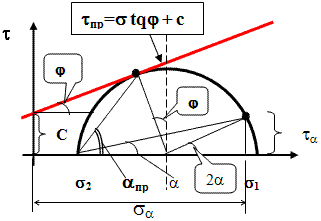
Напряжённое состояние в точке грунта по теории Мора-Кулона. В момент предельного состояния площадка сдвига наклонена к оси абсцисс на угол α_пр.

В момент предельного состояния круг Мора коснется прямой Кулона, тогда легко определить, что внешний угол точки касания составит значение 2α_пр =90° + φ или α_пр = 45° + φ / 2.

Возвращаясь к предыдущей схеме, откладываем значение угла α_пр = 45 + φ/2 от горизонтальной площадки и проводим прямую до пересечения с линией действия главных нормальных напряжений. В результате получаем прямоугольный треугольник с вершиной равной углу β = 45 - φ / 2 – угол между площадкой сдвига и линией действия наибольших главных напряжений.

Таким образом, в момент предельного состояния в основании под нагруженным фундаментом образуются поверхности скольжения, направленные под углом β к линии действия главных нормальных напряжений.

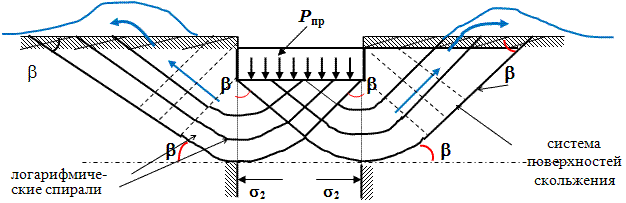
Схема формирования поверхностей скольжения под подошвой жёсткого фундамента в момент предельного состояния, с образованием выпора грунта из-под подошвы на поверхность.

Под подошвой фундамента (штампа) главные нормальные напряжения направлены вертикальны, поэтому угол β будет откладываться от вертикали, образуя под подошвой сеть поверхностей скольжения в виде треугольного ядра (см. схему). За пределами площади загружения, в момент предельного состояния, линии действия главных нормальных σ₂ напряжений горизонтальны (распоры). Тогда угол β (в соответствии с его определением) будет откладываться от горизонтали, образуя сеть (систему) прямолинейных поверхностей скольжения. Поворот главных нормальных напряжений от вертикального положения к горизонтальному вызовет и поворот поверхностей скольжения, которые примут очертания в виде логарифмических спиралей.

В результате в момент предельного состояния под фундаментом мелкого заложения образуется целая система поверхностей скольжения, по которым возникнет движение грунтовых масс с выпором их на поверхность. Данное состояние нагружения соответствует Р_пр и сопровождается развитием резких вертикальных деформаций с нарушением (как правило) устойчивости сооружения (см. ниже приведенную схему).

При Р_пр происходит выпор грунта из-под подошвы фундамента, т.е. развитие пластических деформаций в огромной области.

Подводя итог выше сказанному, на графике осадки от прикладываемого давления можно определить несколько характерных точек (см. ниже приведённую зависимость).

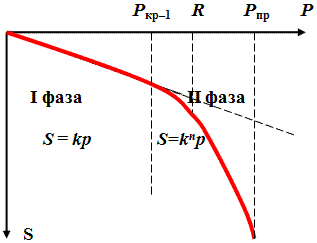
Зависимость осадки фундамента от прикладываемого давления вплоть до предельного состояния.

При напряжениях Р ≤ R (см. график), осадки фундамента считают по линейной зависимости (теория упругости).

При достижении интенсивности давления Р_кр–1 в отдельных точках под подошвой, прежде всего под краями фундамента, возникают зоны предельного равновесия (пластических деформаций τ).

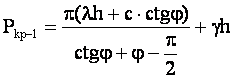
Начальная критическая нагрузка по Пузыревскому Н.П.

Р_kp–1 = f(φ, c, γ, h) – довольно малая величина и принимать её к расчету не выгодно. Поэтому в расчетах приняли, исходя из практики строительства, допускать давление на грунт, при котором зоны пластических деформаций под краями фундамента достигнут глубины ¼ b.

Отсюда ввели понятие R – расчётное сопротивление грунта.

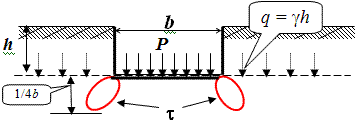
Развитие зон пластических деформаций под углами загруженного фундамента при достижении давления равного расчётному сопротивлению грунта.

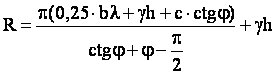
Считать по этой формуле трудоёмко, поэтому ее несколько изменили (в таком виде она имеется в СНиП 2.02.01–83*, формула 7), введя условия совместности работы основания и сооружения.

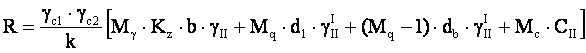
• Где d₁ приведенная глубина заложения фундамента. d₁ = h₁+h₂ γ_п/γ'_II;
• d_b - глубина подвала; d_b ≤ 2 м при В ≤ 20 м; d_b = 0 при В > 20 м
• b - ширина подвала.

Под R понимается такое давление, при котором глубина зон пластических деформаций (зон разрушений) равна ¼ b (подошвы фундамента).