Определение напряжений в массиве грунта от сосредоточенной силы. Задача Буссинеску 1885 г.

Составим расчётную схему данной задачи, представив грунтовое основание, как упругое полупространство.

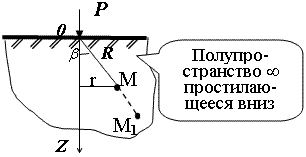
Графическое представление условий (расчётная схема) задачи для определения напряжений в массиве грунта от сосредоточенной силы.

По условиям задачи необходимо определить значения вертикальных напряжений σ_z и касательных напряжений τ_zx; τ_zy в точке М, расположенной на площадке, параллельной плоскости, ограничивающей массив от действия сосредоточенной силы Р.

1. Определим σ_R – в радиальном направлении перпендикулярно R (в т. М)
2. Определим σ_R' – в радиальном направлении (приложенном к площадке, параллельной плоскости ограничивающей массив).
3. Определим σ_z;τ_zx;τ_zy.

Допустим, что под действием силы Р точка М переместилась в точку М₁. Обозначим S – перемещение точки М. Тогда можно записать:

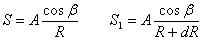
Мы получили перемещение точки М (см. выше приведённый рисунок).

В представленной зависимости осадка точки будет прямо пропорционально завесить от косинуса угла β и обратно пропорционально радиусу расположения точки, где А – коэффициент пропорциональности.

Определим относительное перемещение точки:

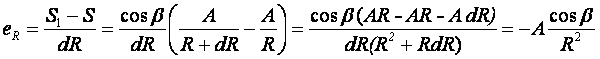
Согласно первому постулату теории упругости между напряжениями и деформациями должна быть прямая зависимость, следовательно:

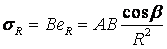
Радиальное напряжение в точке М.

В этой формуле В – коэффициент пропорциональности. Для определения σ_R необходимо определить произведение коэффициентов АВ.

σ_R – определяется по методу, используемому в сопромате («метод сечений»: мысленно разрезают балку, одну часть отбрасывают и оставшуюся часть уравновешивают).

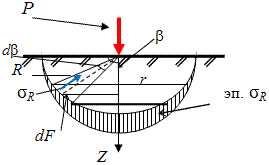
Расчётная схема для определения радиальных напряжений в грунте.

Для решения данной задачи поступим аналогичным образом. Рассматрим полушаровое сечение радиусом R и заменим отброшенное пространство напряжениями σ_R. Рассмотрим изменение β в пределах dβ. Составим уравнение равновесия на ось Z:

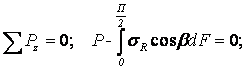
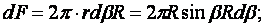
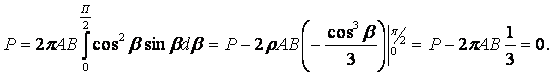
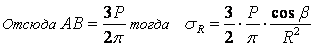
Величина радиального напряжения в грунте зависит от координат точки и величины прикладываемой силы.

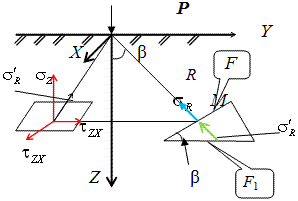
Схема пересчёта радиальных напряжений к вертикальным.

Из геометрических соотношений можно записать:

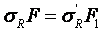
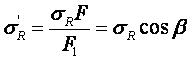
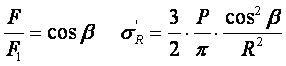
Мы получили величину радиальных напряжений, приложенных к площадке параллельно плоскости, ограничивающей массив.

3 этап решения задачи:

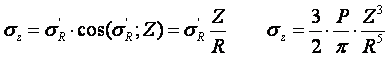
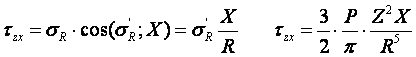
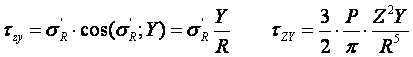
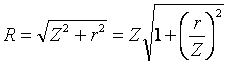, подставим и получим

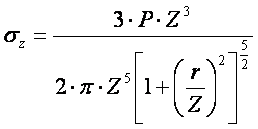
Введём обозначение:

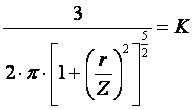
Упрощая выше полученное выражение, вводим значение коэффициента К. Тогда получим:

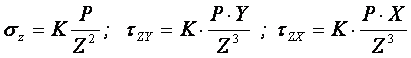
Результат окончательного решения нашей задачи.

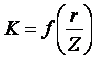– определяется по таблице.