Определение механических характеристик грунтов в приборах трёхосного сжатия

Испытание грунта в приборе трёхосного сжатия ближе отвечает его работе в природных условиях и дает наиболее надежные результаты в определении его прочностных и деформационных свойств.

Трёхосному (объёмному) напряжённому состоянию грунт подвергается в стабилометре.

Ниже приведена схема и общий вид прибора стабилометра, который представляет собой толстостенный цилиндр с помещенным внутри образцом грунта в резиновой оболочке. Образец грунта окружает вода, поэтому при приложении вертикальной нагрузки или давления Р₁, со стороны воды на образец грунта будет действовать боковое давление Р₂.

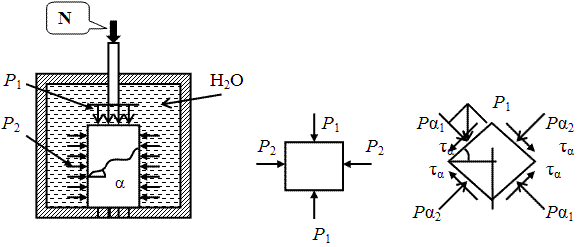
Схема испытаний образца грунта в стабилометре, в условиях объёмного напряжённого состояния.

Общий вид прибора стабилометра.

Таким образом, образец грунта в стабилометре будет находиться в объемно-напряжённом состоянии.

Если вырезать из образца грунта элементарный параллелепипед с гранями перпендикулярно главным нормальным напряжениям Р₁ и Р₂, то такой образец будет испытывать лишь сжатие со всех сторон без возможности разрушения. Однако параллелепипед грунта ориентированный под углом α по своим граням будет испытывать кроме сжимающих усилий Рα еще касательные усилия τ_α (касательные напряжения).

Именно касательные напряжения τ_α вызывают смещение отдельных частиц грунта относительно друг друга и приводят к разрушению образца грунта в целом. В момент такого разрушения или предельного состояния грунта определяются его прочностные и деформационные свойства.

Проведение испытаний или доведение образца грунта до разрушения (предельного состояния) зависит от соотношения значений главных нормальных напряжений и условий испытаний.

В практике исследований используется большое число стабилометров различной модификации и размеров в зависимости от решения поставленной задачи. Так на левой фотографии представлен прибор стабилометр, предназначенный для исследования мелкодисперсных грунтов. На правой фотографии также представлен стабилометр, но уже для исследования крупнодисперсных грунтов.

Напряжённое состояние в элементарном образце грунта (в данной точке) весьма наглядно отображается при помощи эллипса напряжений, построенного на осях главных напряжений.

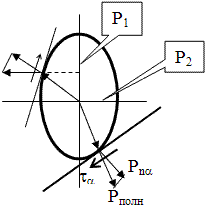
В этом случае любая точка на эллипсе (за исключением точек, расположенных на его осях) будет испытывать как нормальные Р_α, так и касательные напряжения τ_α или полные напряжения Р_полн., величина которых будет изменяться в пределах от Р₂ до Р₁.

Р₁ ≥ Р_полн ≥ Р₂

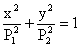- Общее уравнение эллипса.

Наиболее просто напряжённое состояние в точке грунта М может быть выражено кругом Мора (сопротивление материалов).

Круг Мора (достаточно изобразить его половину) строится на оси абсцисс Р с диаметром, равным разности величин главных нормальных напряжений Р₁ – Р₂. Тогда ордината любой точки М на круге Мора будет определять величину касательных напряжений τ_α в этой точке.

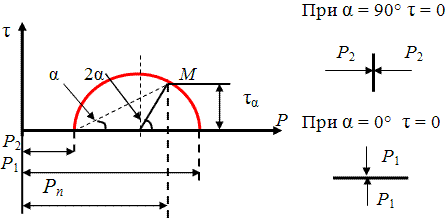
Круг Мора - графическое представление изменений напряжений в точке грунта в зависимости от ориентации рассматриваемой площадки.

Положение точки М или угол наклона рассматриваемой площадки будет определяться углом α. Рассмотрим граничные изменения угла α:

• При α=0° точка М будет расположена на оси Р в точке, соответствующей напряжению Р₁ (горизонтальная площадка), касательные напряжения здесь будут равны 0, а следовательно разрушение невозможно.
• При α=90° точка М также будет расположена на оси Р в точке, соответствующей напряжению Р₂ (вертикальная площадка), касательные напряжения здесь будут равны 0, а следовательно разрушение невозможно.

Поскольку предельное состояние (разрушение в грунте) возникает от действия касательных напряжений, то оно может произойти тогда, когда точка М (ее положение) коснется прямой Кулона, прямой предельного состояния грунта.

В процессе испытаний оставляем неизменным Р₂ и увеличиваем Р₁. Максимальное значение Р₁ будет, когда круг Мора коснется прямой Кулона.

Описанная методика испытаний схематично представлена на нижерасположенном левом рисунке.

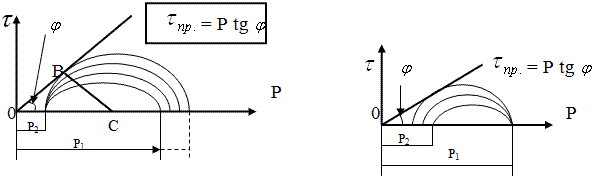
Может быть применена и другая методика испытаний:

В процессе испытаний оставляем неизменным Р₁ и уменьшаем (сбрасываем боковое давление) Р₂. Минимальное значение Р₂ будет, когда круг коснется прямой Кулона. Данная методика испытаний также схематично представлена в правой части рисунка.

Из представленной схемы в момент предельного состояния, когда точка М круга Мора коснется прямой Кулона (точка В на левом рисунке), можно записать, что треугольник ОВС – прямоугольный, ВС – радиус, тогда:

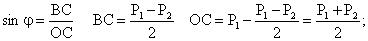
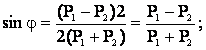
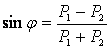– уравнение, описывающее предельное сопротивление грунта сдвигу при трёхосном напряжённом состоянии (для сыпучих грунтов).

Для связных грунтов необходимо подобным образом испытать не менее двух образцов с различной величиной главных напряжений 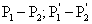. (см. нижеприведенную схему)

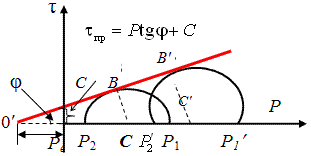
Схема результатов испытаний связных грунтов в стабилометре.

Из представленного рисунка можно определить давление связности Р_е (суммарно заменяющее действие сил сцепления).

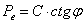
Выполняя аналогичные геометрические построения, что и в предыдущем случае, для прямоугольного треугольника О'В'С получим:

– уравнение, описывающее предельное сопротивление грунта сдвигу при трёхосном напряжённом состоянии (для связных грунтов).