Для решения задачи по определению осадки фундамента, рассмотрим схему работы двух
фундаментов с разной шириной подошвы, но передаваемых одинаковое давление (Р) на
основание (см. схему).
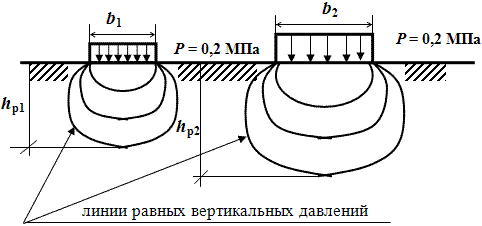
Схема уплотнения основания для фундаментов с разной шириной подошвы.
При большей площади загрузки основания (большей ширине подошвы фундамента) глубина
распределения давлений и объём грунта, подвергающийся деформации будут больше. Следовательно,
и осадки будут больше.
Нельзя ли рассчитать осадку фундамента по известной формуле S=hmvp
– как осадку при сплошной нагрузке?
В этом случае, необходимо определить точную толщину сжимаемого слоя hэкв.,
которая отвечала бы осадке фундамента, имеющего заданные размеры.
Эквивалентным слоем грунта будем называть такой слой, осадка которого при сплошной
нагрузке в точности равна осадке фундамента на мощном массиве грунта (полупространстве).
В соответствии с приведённым выше сформулированным определением, будем иметь две
схемы деформирования основания:
- Слой грунта толщиной h при сплошной нагрузке (левая схема на нижерасположенном рисунке).
- Осадка фундамента на упругом полупространстве (правая схема на нижерасположенном
рисунке).
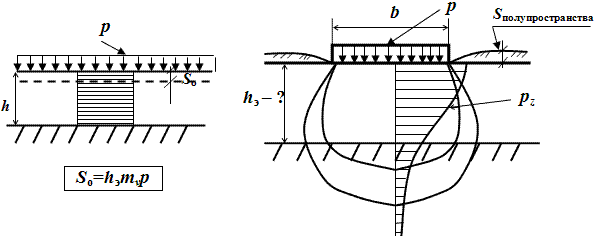
Расчётные схемы для определения эквивалентного слоя грунта для фундамента заданного
размера.
Тогда для первой схемы будем иметь величину осадки S0=hэ
mv p.
Для второй схемы осадка фундамента может быть определена по формуле Шлейхера-Буссинеску:
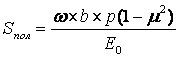
По условиям определения эквивалентного слоя, осадки по 1 и 2 схемам деформирования
равны
S0 = Sпол
Тогда приравнивая правые части выражений осадок по 1 и 2 схемам, получим:
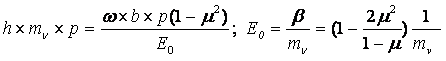
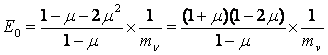
Подставляем полученное выражение для модуля общей деформации в исходную формулу
и произведя преобразования, получим значение толщины эквивалентного слоя hэкв
и осадки фундамента с использованием hэкв :
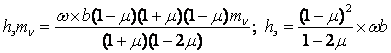
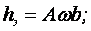
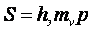
Осадка фундамента по методу эквивалентного слоя при однородном напластовании грунтов.
Значения коэффициентов Аω определяются по табличным данным, представленных
в учебниках Н.А. Цытовича.
Данный метод расчета осадки фундамента имеет точное решение при следующих допущениях.
- Однородный грунт имеет бесконечное распространение в пределах полупространства.
- Деформации в пределах полупространства, пропорциональны напряжениям, т.е. полупространство
линейно деформируемо.
- Деформации полупространства устанавливаются методами теории упругости.
- Ограничения: Fфунд ≤ 50 м2, Ноднородн.гр
≥ 30¸40 м.
В качестве примера использования данной методики рассмотрим осадку фундамента при
однородном напластовании грунтов и следующих исходных данных:
|
Исходные данные
|
Вычисление
|
|
h=2 м; а = в = 3 м
Рф=2,5 кг/см2 =0,25МПа
(фактическое давление под подошвой грунта)
g = 1,8 т/м3 = 18кН/м3
μ = 0,3 суглинок
m0 = 0,04 см2/кг = 40·10–5 м2/кН
е = 0,9
S = ?
|
S = hэmvp; μ = 0,3; a/b = 1
hэ = Aωb.
Из таблицы находим Aω = 1,08;
hэ = 1,08·300 = 324 см = 3,24 м;
mv=m0/(1+e)=0,04/1,9=0,02 см2/кг;
Р – дополнительное уплотняющее давление
P = Pф – γ0h = 25– 1,8·2 = = 21,4 т/м2 =2,14
кг/см2.
S = 324×0,02×2,14 ≈ 14 см
|
Таким образом, осадка фундамента (S) может быть вычислена быстро и достаточно точно.
Вычисленная величина осадки S = 14 см – много это или мало?
Сравнивая полученную величину осадки с предельными значениями (Sпред
= 8…12 см), для проектируемого сооружения по СНиП 2.02.01–83*, не трудно заметить,
что расчётная осадка значительна, т.е. S> Sпред. Очевидно, что полученное
решение прямо пропорционально зависит от сжимаемости основания, для наших условий
грунт был принят средне сжимаемым mv = 0,02 см2/кг.