Метод Жемочника для расчета фундаментных балок на упругом основании

В основу метода, предложенного Жемочкиным Б.Н., положены следующие допущения:

1. Действительная криволинейная эпюра распределения давлений под подошвой балки заменяется ступенчатой (см. схему).

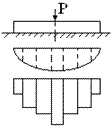
Схема первого принятого допущения для расчёта балок по методу Жемочкина Б.Н.

2. Распределение давлений на ширине балки также принимаются равномерным.

3. Между балкой и сжимаемым основанием предполагаются жесткие шарниры опирающиеся стержни, воспринимающие усилия от балки и равномерно распределяющие это усилие на основание.

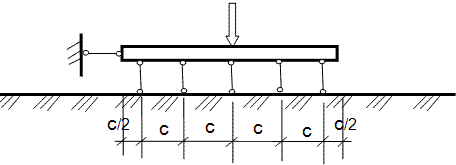
Схема третьего принятого допущения для расчёта балок по методу Жемочкина Б.Н.

4. Условие совместимости работы балки и основания и удовлетворяются равенством прогиба балки и осадки основания в месте закрепления опорного стержня y_i = S_i .

Этот метод является универсальным и позволяет решать любые задачи с любой степенью сложности.

Используя принятые обозначения (см. выше), получим расчётную схему, в которой шарнирные стержни заменены на неизвестные реакции опор X_i, при этом балка получает вертикальное смещение Y₀ и возможный поворот на угол φ₀.

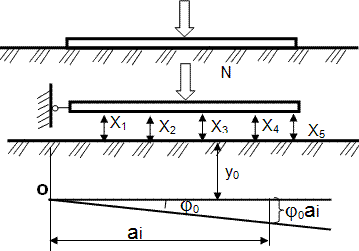
Расчётная схема балки на упругом основании по методике Жемочкина Б.Н. (смешанная задача строительной механики).

В соответствии с правилами строительной механики составляется система канонических уравнений:

Для решения данной системы уравнений необходимы дополнительно два уравнения равновесия:

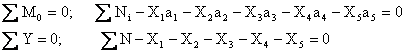
В итоге задача решается смешанным методом.

Здесь Δ_ki - единичное перемещение по направлению "к" связи от воздействия "i" связи:

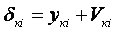
• Y_ki - единичное перемещение, вызванное осадкой основания;
• V_ki - единичное перемещение, вызванное прогибом балки;
• Y_ki, V_ki - находятся обычно по таблицам.

Решив систему уравнений и найдя X_i, определяют величины реактивных давлений Р_i, соответствующих ширине принятых участков ступенчатой эпюры (см. схему и допущение № 1):

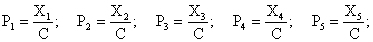
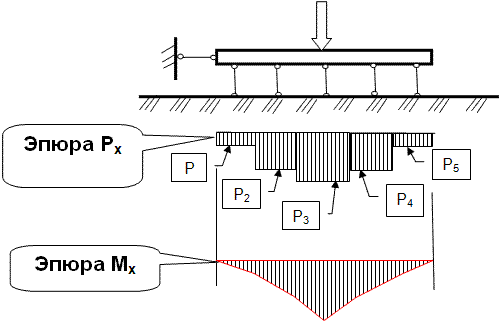
Затем, с использованием метода сечений, строят эпюры изгибающих моментов, а по ним окончательно определяют сечение балки и ее армирование.

Область применения:

1. При хороших (плотных) грунтах.
2. Для расчета плит (днища емкостей).
3. При глубоком залегании скалы.

Следует отметить, что точность решения поставленной задачи зависит от количества принятых опорных стержней. Чем больше принятых опорных стержней, тем точнее результат решения в описании ступенчатой эпюры реактивных давлений и, следовательно, в вычислении изгибающих моментов. Однако увеличение опорных реакций (неизвестных X_i) приводит к усложнению задачи, так как возрастает система канонических уравнений. Для преодоления данного противоречия составлены расчётные программы, позволяющие получать решение задачи практически с любой заданной точностью.