Численный пример по предлагаемой методике расчёта

Представленная интерпретация графического решения рассматриваемой методики (рис. 2, 3), может быть рассмотрена и в аналитической форме. Решения осуществляем по программе автора «BRNL», размещённой на сайте: http://www.buildcalc.ru/.

Для примера выполним расчёт куста столбчатого условного свайного фундамента, при длине свай 12 м и вертикальной расчётной нагрузи в 4350 кН. Основные исходные данные, а также грунтовые условия, с модулем деформации основания в 20 МПа, представлены в нижерасположенной табличной форме. Следует подчеркнуть, что расчёт условного свайного фундамента, с учётом не линейной работы основания, (рис. 4) производится по двум предельным состояниям, с определением (две последние строки в табл. «Рассчитанные данные по основанию») коэффициента надёжности и величины осадки, которая может, как задаваться, так и определяться по заданным размерам подошвы. Используя последнее условие, получим:

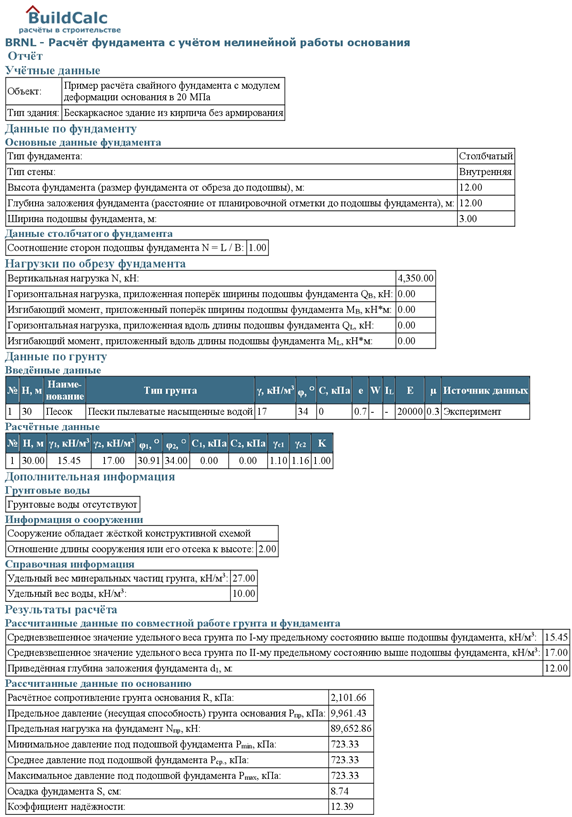
Рис. 4. Пример результатов расчёта куста условного свайного фундамента по двум предельным состояниям, с учётом не линейной работы основания с модулем деформации в 20 МПа.

Следует подчеркнуть, что не линейная работа основания, за счёт развития зон пластических деформаций под подошвой условного фундамента глубокого заложения, обусловлена в основном величиной предельного давления грунта основания (несущая способность), которая составляет: Р_пр. = 9961.43 кПа (рис. 4, вторая строка табл. «Рассчитанные данные по основанию»). Для объективной оценки данных вычислений, выполним расчёт для данного условного фундамента глубокого заложения по методике Березанцева В.Г. [5], где Р_пр. (в соответствии с нашими принятыми обозначениями) рекомендуется вычислять по следующей формуле:

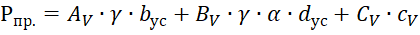
где, A_V, B_V, C_V – табличные коэффициенты, определяемые в зависимости от (φ) угла внутреннего трения грунта основания; α – коэффициент, определяемый по графической зависимости; Υ- объёмный вес грунта основания; с_V - сцепление основания.

Численный результат решения по формуле (4), с использованием исходных данных рассматриваемого примера, позволяет получить следующий результат:

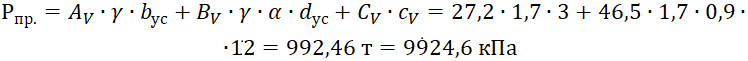
Нетрудно заметить, что решения по методике Березанцева В.Г., формула (4) и по предлагаемой методике с использованием программы «BRNL» в определении Р_пр., имеют расхождения не более 1%, что объективно подтверждает достоверность принятых допущений в основе рассматриваемого метода.

Необходимо отметить, что программные решения могут быть многократно повторены при любых изменениях начальных условий, рассматриваемой задачи. Это позволяет провести анализ и оптимизацию получаемых решений. Пример интерпретации такого подхода представлен в графическом виде на рис. 5.

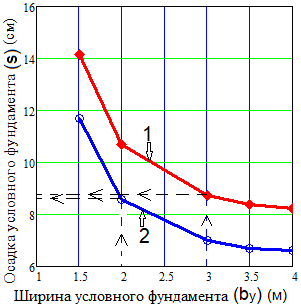
Рис. 5. Расчётная зависимость осадки (S) куста условного свайного фундамента от его ширины (b_у), по условиям рассматриваемого примера. 1 – основание с модулем деформации в 20 МПа; 2 - основание с модулем деформации в 25 МПа.

Результаты решений программного расчёта (рис. 5) позволяют построить графические зависимости осадки (S) условного свайного фундамента от его ширины (b_у) или 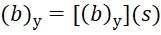. В данном примере построены две кривые 1 и 2 (рис. 5), отличающиеся деформационными свойствами оснований. При анализе полученных зависимостей, очевидно, что для кривой 1 при ширине подошвы условного свайного фундамента (b_у) ≥ 3м осадка данного условного свайного фундамента (S) практически стабилизируется в размере 8,5 см, для кривой 2 (основание с модулем деформации в 25 МПа) подобная оптимальная осадка составляет около 7 см.

Таким образом, данные величины осадок следует считать оптимальными для рассматриваемых грунтовых условий и действующих нагрузок.

Анализируя полученные зависимости (рис. 5) по условиям одинаковой (допустимой для данного вида сооружения) осадки, не трудно заметить:

• для основания с модулем деформации в 20 МПа (кривая 1 или для 1 фундамента), при осадке 8,74 см ширина подошвы условного свайного фундамента составит 3 м.
• для основания с модулем деформации в 25 МПа (кривая 2 или для 2 фундамента), при осадке 8,56 см ширина подошвы условного свайного фундамента составит 2 м.

Следовательно, и 1 и 2 свайные фундаменты будут давать практически одинаковую осадку (с минимальной неравномерностью относительной осадки), с соответствующей требуемой шириной условного фундамента b_у(т1) = 3м и b_у(т2) = 2м.

Определив, таким образом, ширину подошвы требуемых условных свайных фундаментов b_у(т1,2), нетрудно найти площадь (А_ус) подошвы кустовых столбчатых условных фундаментов и, используя формулу (3), рассчитать необходимое (n) число свай:

.

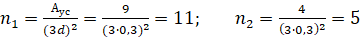Таким образом, по условиям рассматриваемого примера, два свайных фундамента, устраиваемые в основаниях с модулем деформации в 20 МПа и 25 МПа, для получения практически одинаковой осадки в размере около 8,6 см, должны иметь соответственно минимальное количество 11 и 5 забивных свай сечением 30х30 см.

Следует подчеркнуть, что проектирование свайных фундаментов по величине задаваемой осадке (II предельное состояние) позволяет снизить неравномерность относительной осадки рядом расположенных фундаментов до минимальных допустимых значений (учёт неоднородности грунтовых оснований и различной степени нагружения), что создаёт наиболее благоприятные условия для работы надземных конструкций сооружения.

Для внецентренно нагруженных свайных фундаментов, представленную методику необходимо дополнить определением горизонтальной составляющей в уровне головы свай и выполнить расчётную проверку ж/б стволов свай на изгиб в соответствии с рекомендациями СП 24.13330.2011 [6].