Графическая интерпретация результатов расчёта

На основе второго принятого допущения, используя выражение (1), представляется возможность, задаваясь предварительно различной величиной (b_у) (рядовое расположение свай под стену или условная ширина подошвы свайного куста), построить графики расчётной зависимости S_i = S_i(P_i) (рис. 2).

Решения в соответствии с уравнением (2) может быть реализовано в виде расчётных графических зависимостей P_i = P_i(b_уi), которые для различных расчётных сечений (N-N) свайного фундамента в зависимости от нагрузки, представлены кривыми 1-1, 2-2, 3-3 (рис. 3).

В соответствии с условиями поставленной задачи, задаёмся величиной осадки, при которой будем рассчитывать свайный фундамент. Графическая интерпретация такого решения представлена на рис. 2. Тогда, по заданной осадке (S_A) (см. стрелочную идентификацию на рис. 2), находят значения давлений Р₁, Р₂, Р₃, соответствующие b_у1, b_у2, b_у3 – задаваемым величинам ширины подошвы условного фундамента.

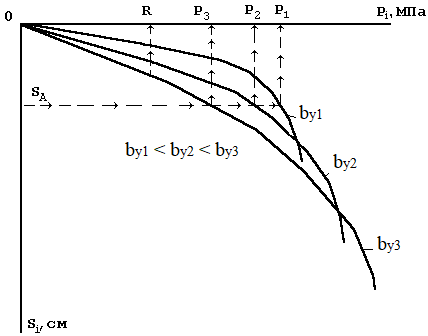
Рис. 2. Графики расчётной зависимости (1) осадки (S_i) от прикладываемого давления (P_i) на основание; b_у1, b_у2, b_у3 – задаваемая величина ширины подошвы условного фундамента.

Найденные пары значений P₁ и b_у1; P₂ и b_у2; P₃ и b_у3 из решений на рис. 2, наносят на график P_i=P_i(b_уi) (рис.3) в виде отдельных точек, соединяя которые получаем кривую А, соответствующую равной заданной осадки (S_A).

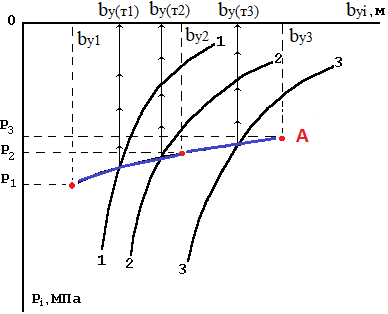
Рис. 3. Графики  расчётной зависимости (2) P_i= P_i(b_уi); 1-1, 2-2, 3-3 – кривые давлений для  различных расчётных сечений (N-N) свайного фундамента в зависимости от нагрузки; А – кривая равной заданной осадки S_A; b_у(т1), b_у(т2), b_у(т3), - размеры требуемой ширины подошвы условного фундамента.

Совместное решение или пересечение кривых давлений 1-1, 2-2, 3-3 для различных расчётных сечений свайного фундамента в зависимости от нагрузки и возможного изменения ширины подошвы условного фундамента (рис. 3) с кривой А – определит требуемые размеры подошвы условных свайных фундаментов b_у(т1), b_у(т2), b_у(т3), соответствующие равной заданной осадки (S_A).

Следует подчеркнуть, что все, представленные на рис. 3, расчётные значения свайных фундаментов будут иметь различные размеры подошвы условных свайных фундаментов b_у(т1), b_у(т2), b_у(т3), но обладать практически одинаковой осадкой.