Практическое значение определение напряжений σz в массиве грунта
важно для прямоугольного в плане фундамента.
Изобразим загруженную поверхность в плане (рис. 2).
Совместим оси координат с центральными осями прямоугольника, ограничивающего загруженную
давлением Р (кПа) поверхность. Обозначим размеры прямоугольника: L, B – длина и
ширина; l, b – полудлина и полуширина. Выделим на загруженной поверхности бесконечно
малую площадку с координатами в центре площадки ξ и η, и площадью dξ ·
dη.
Элементарная сила, действующая на площадку, будет равна: dP = p · dξ ·
dη.
Определим напряжение dσz в грунтовом массиве в точке с координатами
x, y, z от элементарной силы dP, воспользовавшись формулой Ж. Буссинеска (1):
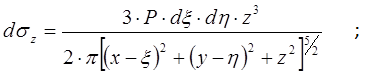 (5)
(5)
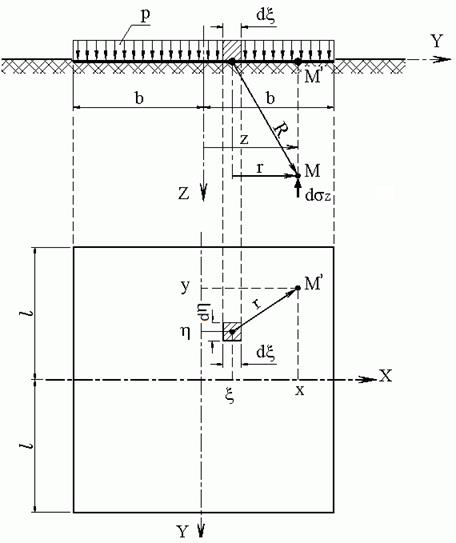
Рис. 2. Расчётная схема для определения напряжений от нагрузки, распределенной по
прямоугольнику: Р – интенсивность нагрузки; l, b – полудлина и полуширина площади
нагрузки.
В формуле (5) учтено, что радиус-вектор R соединяет точку с координатами x, y, z,
в которой определяется напряжение, и точку с координатами ξ, η, 0, в которой
действует элементарная сила. Для определения напряжения σz в точке
с координатами x, y, z от всей загруженной площади проинтегрируем выражение (5)
по загруженной площади:
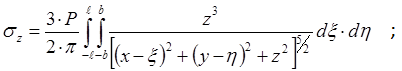 (6)
(6)
Интеграл по формуле (6) имеет замкнутое аналитическое решение в тригонометрических
функциях, впервые полученное в 1935 г. А. Лявом [1].
Наиболее простые выражения данного интеграла для вертикальных напряжений определяются
в сечении под центром тяжести загруженной площади:
σz = α · Р,
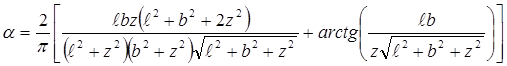 (7)
(7)
Значения коэффициента α, зависящего от координат рассматриваемой точки, может
определяться по формуле (7) или с использованием таблиц, представленных в нормативно-справочной
литературе.