Методика расчёта

В развитие ранее рассмотренной методики [2, 3], построенную ломанную кривую (а) – учёта развития объёмов зон пластических деформаций (V_i) (рис. 1.), можно представить в виде непрерывной, относительно плавной зависимости. В этом случае, отказавшись от расчётного сопротивления грунта основания (R), примем допущение, что интервал давлений (Рпр. - Рн.кр.), к примеру, можно разбить на конечные малые отрезки _ΔPi = 0,2Рн.кр. Количество отрезков (n) определится из отношения:

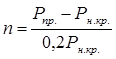(2)

Тогда ордината (V_o´), соответствующая объёму развития зон пластических деформаций при давлении равном 1,2 Р_н.кр. (вместо R, из условий построения на рис. 1.), может быть получена из следующего выражения:

(3)

Для ординаты (V_i), соответствующей объёму развития зон пластических деформаций при давлении (P_i), получим:

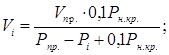(4)

где

P_i = P_н.кр. (1+0,2i), при i = 1…n. (5)

Таким образом, не представляет труда, найти коэффициент нелинейности упругопластического деформированного основания (K_i´), при непрерывном, плавном изменении расчётной траектории (а) развития объёма зон пластических деформаций в основании, как отношение (V_i) к (V_o´):

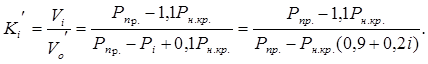(6)

Тогда, на основе выше изложенного, представляется возможным осадку упругопластического основания (S_i) для фундамента заданного размера, при давлениях Pi превышающих 1,2Pн.кр., определить по формуле:

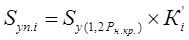(7)

где S_{y(1,2Рн.кр.)} – осадка линейно-деформированного полупространства при давлении соответствующем 1,2Pн.кр.,определяемая по формуле Ф. Шлейхера [3]. Из выражения (7) может быть определён коэффициент нелинейности упругопластического деформированного основания (K_i´):

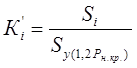(8)

Тогда, приравнивая правые части уравнений (6) и (8), получим:

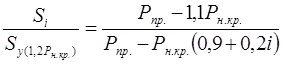(9)

В принятом выражении (5) величина давления Р_i может быть приравнена к среднему давлению под подошвой ленточного фундамента, т.е. Р_i = N/b, где N – нагрузка, действующая по подошве фундамента шириной подошвы b. Подставляя данные условия в выражение (5), получим:

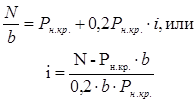(10)

Подставляя полученное значение i из условия (10) в уравнение (9), а также заменяя S_{y(1.2Рн.кр.)} по решению Ф. Шлейхера, получим:

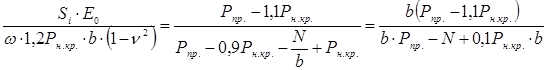(11)

Решая уравнение (11) относительно ширины подошвы фундамента (b), можно записать:

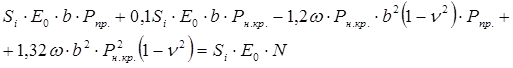
Подставляя значения 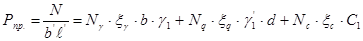– вычисляемые по формуле В.Г. Березанцева, В.В. Соколовского [4], где 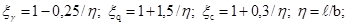ℓ – ширина подошвы фундамента, получим:

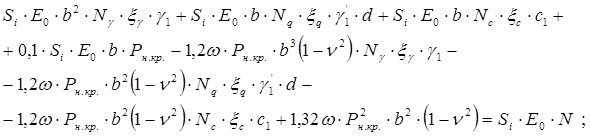
Учитывая, что

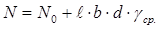
где N₀ – нагрузка по обрезу фундамента; γ_ср. – среднее значение объёмного веса материала фундамента и грунта на его уступах. Запишем данное уравнение относительно (b), тогда получим:

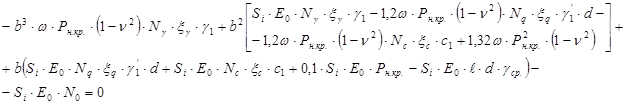(12)

Полученное кубическое уравнение (12) позволяет вычислить ширину подошвы (b) ленточного фундамента. При решении такого уравнения, с использованием метода Виета-Кардано, получаем три корня и выбираем действительное значение соответствующие заданной величине осадки S_i и степени нагружения N₀ ленточного фундамента.

При решении уравнения (12) необходимо задаваться величиной осадки (S_i), по величине которой и производится расчёт необходимой ширины b) подошвы фундамента с учётом нелинейной работы основания в упругопластической стадии деформирования.