Для большей наглядности воспользуемся графическим методом изображения измеренных
значений глубин промерзания грунта, на бумаге с вероятностной шкалой, в прямоугольной
системе координат, разработанным А. Хазеном [5].
Построив по результатам измерений для метеостанции г. Иркутска номограмму расчёта
максимальных глубин промерзания под оголённой поверхностью различной степени вероятности
F (рис. 2), получим:
- Максимальную глубину промерзания грунта, возможную раз в 10 лет – 281 см (F = 10%);
- Раз в 20 лет – 284 см (F = 5%);
- Раз в 50 лет – 287 см (F = 2%).
Все эти значения существенно превосходят средний максимум, вычисленный за тот же
период обычным способом (рис. 1).
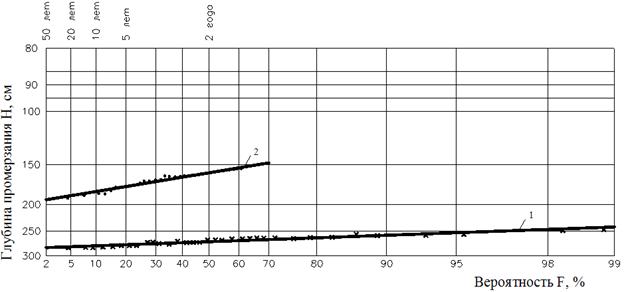
Рис. 2. Номограмма для расчёта максимальной глубины промерзания грунта на метеорологической
станции г. Иркутска: 1 – оголённая поверхность (по годовым максимумам); 2 – поверхность
с естественным покровом (по формуле Пуассона, с вероятностью промерзания Н ≥
150 см).
Поскольку период наблюдений за глубиной промерзания на большинстве метеорологических
станций мал (< 25 лет), то для получения вероятностных значений целесообразно
воспользоваться законом Пуассона. Проведя расчёты по этому методу для поверхности
с естественным покровом, и нанеся их на бумагу с вероятностной шкалой, получим номограмму
для расчёта максимальных глубин промерзания различной вероятности (рис. 2). Полученные
расчётом величины максимальных глубин промерзания грунта, возможные раз в 10, 20
и 50 лет, также будут значительно превосходить средний максимум, вычисленный за
тот же период обычным способом (рис. 1).
Таким образом, в районах глубокого сезонного промерзания для получения надёжных
данных по величине глубины промерзающего слоя грунта наиболее целесообразно в расчётах
подходить с вероятностной оценкой имеющихся значений в зависимости от ответственности
возводимого сооружения.