Теоретическое обоснование увеличения несущей способности усиленного основания

Практически любая реконструкция зданий Санкт-Петербурга, имеющих историю своего существования в 100…200 лет и более, неизбежно связана с решением ряда вопросов по надежности существующих фундаментов и их оснований.

В последнее время на многих реконструируемых объектах Санкт-Петербурга в качестве конструктивного элемента увеличения несущей способности основания существующих фундаментов стали применять выштампованные микросваи. Такие микросваи (длиной до 2…2,5 м) являются конструктивным элементом усиления основания, представленного позднеледниковыми и послеледниковыми озерными и морскими отложениями (пылеватые пески, супеси, суглинки), имеющими довольно низкие несущие свойства и высокую водонасыщенность.

Методика выполнения данных свай [1] заключается в следующем:

1. Из подвала реконструируемого здания вдоль его несущих стен пневмопробойником в основании пробиваются вертикальные или наклонные скважины диаметром 130…155 мм.
2. Многократная проходка (до 10 раз) таких скважин пробойником сопровождается подачей и вбиванием сухой бетонной смеси.
3. В образовавшуюся полость подаётся жёсткая бетонная смесь и производится армирование.
4. В результате в основании создаётся свая диаметром 200…250 мм и длиной до 2…2,5 м [4].

Ставится задача определения степени усиления основания закреплённого микросваями. С этой целью изобразим схему зон предельного состояния основания для ленточного фундамента (левая часть рисунка 1).

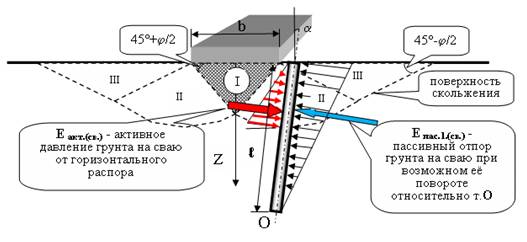
Рис. 1. Расчётная схема формирования предельного состояния от полосовой нагрузки для основания, усиленного выштампованными микросваями, до начала поворота относительно т. О. I – зона переуплотнённого грунта в виде клина; II – зона развития пластических деформаций (сдвигов в условиях предельного состояния); III – зона с непрерывными поверхностями скольжения (формирование выпора).

Для ленточного фундамента предельная нагрузка на основание может быть определена выражением 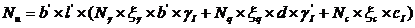1:

, (1)

где все обозначения приняты в соответствии со СНиП [3];

В правой части рисунка 1 изображена расчётная схема (по Л. Прандтлю) от полосовой нагрузки для основания, в которое в качестве усиления добавлена выштампованая микросвая.

Выполненные микросваи с целью усиления (увеличения силы предельного сопротивления) основания вдоль существующих фундаментов пересекают зону II (рис.1) и таким образом, прежде всего, создают препятствие для развития горизонтальных деформаций (зон сдвигов). В результате на часть длины микросваи Z_max будет действовать горизонтальный распор, создавая усилие в виде активного давления грунта Е_{акт.(св.)}. Величина данного распора переменна в зависимости от условий загружения фундамента и достигает максимального значения в момент нарушения равновесия жёсткой сваи (поворот относительно т. О).

Противодействовать силе активного давления грунта будет пассивный отпор Е_пас1св, развитие которого может быть в первом приближении определено двумя этапами. Первый этап работы продолжается до возникновения перемещений микросваи относительно т. О (до момента предельного равновесия Е_акт.св=Е_пас1св). На данном этапе пассивный отпор развивается по всей длине l микросваи (рис. 1).

Для определения Е_пас1св вычислим пассивное давление s_2пас в грунте, действующее на сваю из условия предельного состояния (формула 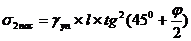2):

, (2)

Тогда пассивный отпор может быть определён выражением 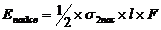3:

, (3)

где γ_уп. – удельный вес грунта вокруг сваи, с учётом его уплотнения в процессе изготовления микросваи, принято что γ_уп=1,11g [4];

l – длина микросваи;

j – угол внутреннего трения грунта основания;

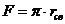– площадь половины периметра микросваи, по которой возникает пассивный отпор;

r_св – радиус изготовленной микросваи.

Подставляя введённые обозначения в выражение 3, получим выражение 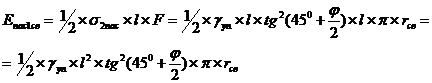4:

(4)

Пассивный отпор Е_паc1св в соответствии с геометрическими построениями (рис. 2) может быть представлен двумя составляющими:

1. Нормальным давлением на ствол микросваи: Е_пас1св ´ cosa.
2. Трением грунта вдоль ствола микросваи: Е_пас1св ´ sina.

Здесь a – угол наклона микросваи к вертикали.

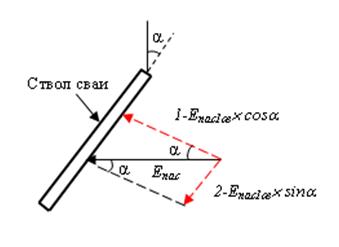
Рис. 2. Геометрическое разложение пассивного отпора на две составляющие.

Определив величину пассивного отпора для микросваи в момент её предельного равновесия (возникновение поворота относительно т. О), представляется возможным вычислить дополнительную составляющую для силы предельного сопротивления усиливаемого микросваями основания (формула 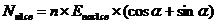5):

, (5)

где n – количество микросвай усиления на единицу расчётной длины фундамента.

Тогда для основания, усиленного микросваями, сила предельного сопротивления (из условия равновесия свай) составит (выражение 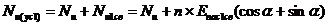6):

, (6)

где N_u – сила предельного сопротивления основания, без учёта свай, определяемая выражением (1).

N_u1с – сила предельного сопротивления основания с учётом работы микросвай (предельное состояние микросвай относительно точки О).

Таким образом, задавшись предварительно размерами микросваи (радиусом и длиной, по технологическим особенностям изготовления), можно найти необходимое число микросвай усиления (n) (из выражения 7), в зависимости от требуемой (задаваемой) величины силы предельного сопротивления усиленного основания N_u(ус1) (из условия равновесия свай):

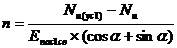. (7)

Второй этап работы усиленного основания возникает после начала деформации микросваи относительно т. О (момент нарушения устойчивости). В этот момент предполагается, что поверхности скольжения грунта (в направлениях от фундамента) начинают плавное обтекание вокруг микросвай. В результате происходит резкое уменьшение развития площади влияния сопротивления пассивного отпора на максимальную глубину развития зон пластических деформаций (по расчётам, сделанным для разных диаметров микросвай, площадь развития пассивного отпора уменьшается более чем в 12 раз) [5].

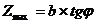Как известно, максимальная глубина развития зон пластических деформаций при полосовой нагрузке, согласно исследованиям Маслова Н.Н. [2], может быть определена выражением 8:

, (8)

где b – ширина подошвы полосовой нагрузки.

Исходя из перечисленных условий, до глубины Z_max пассивным отпором в первом приближении можно пренебречь (значительное снижение сопротивления грунта). Тогда пассивный отпор Е_паc2св будет возникать на части сваи h, расположенной ниже поверхностей скольжения (рис. 3).

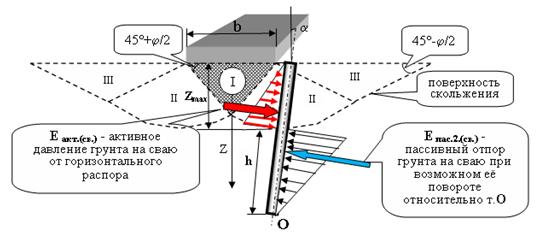
Рис. 3. Расчётная схема формирования предельного состояния от полосовой нагрузки для основания, усиленного выштампованными микросваями, после начала поворота относительно т. О. I – зона переуплотнённого грунта в виде клина; II – зона развития пластических деформаций (сдвигов в условиях предельного состояния); III – зона с непрерывными поверхностями скольжения (формирование выпора).

Для определения Е_пас2св. вычислим пассивное давление s_2пас. в грунте, действующее на сваю из условия предельного состояния (формула 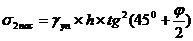9):

. (9)

Тогда пассивный отпор может быть определён выражением 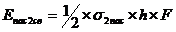10:

, (10)

где h=ℓ-b´tgφ – отрезок сваи, расположенный ниже поверхностей скольжения (см. ранее).

Преобразуя выражение 10, получим (формула 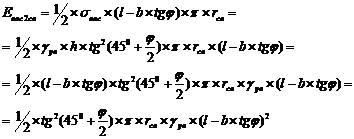11):

. (11)

Таким образом, как только возникнет условие Е_акт.св>Е_пас1св, микросвая получит смещение (поворот и перемещение вдоль ствола), следовательно противодействовать Е_акт.св будет пассивный отпор Е_пас2св (формула 12):

В результате представляется возможным вычисть дополнительную составляющую для силы предельного сопротивления усиленного микросваями основания (N_uс2св) на втором этапе работы (см. ранее):

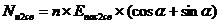. (12)

Тогда для основания, усиленного микросваями, сила предельного сопротивления (с учётом перемещения микросваи) по аналогии с выражением 6 составит (формула 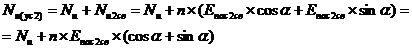13):

. (13)

Как показывает расчётный анализ значение силы предельного сопротивления основания N_u(ус2), на основании вычислений меньше величины N_u(ус1). Следовательно силу предельного состояния основания N_u(ус2) и соответствующее ему предельное давление следует рассматривать как величину, имеющую только теоретический интерес.

Расчёт необходимого количества микросвай усиления следует осуществлять исходя из величины N_u(ус1), т.е. до момента нарушения условия равновесия свай (см. выражение 7).