В настоящее время инженерно-геологические испытания грунтов оснований, характеристики
которых являются основой для решения любых геотехнических задач, проводятся, как
правило, по стандартным методикам. Такие испытания часто бывают, не адекватны фактической
работе оснований при рассмотрении конкретных геотехнических задач.
Рассмотрим геотехническую задачу проектирования фундамента на естественном основании.
Для определения расчетного сопротивления грунта основания необходимо, прежде всего,
знать его прочностные характеристики: угол внутреннего трения и величину сцепления.
Данные величины обычно определяются изыскательской организацией на основе стандартных
сдвиговых испытаний в условиях плоской задачи. Для этого из пробуренных скважин
отбирают керны (монолиты грунта), из них в лабораторных условиях вырезают кольца,
ориентированные обычно параллельно горизонтальной поверхности и проводят сдвиговые
испытания. Подобные испытания лишь в малой степени отражают реальную работу несущего
слоя основания под подошвой проектируемого фундамента.
Хорошо известно (Федоров И.В., Малышев М.В., Мурзенко Ю.Н. и др.), что при передачи
под подошвой фундамента давления Pi > Pн.кр. в основании
развиваются зоны (области) пластических деформаций, где:
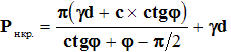
|
(1)
|
Pн.кр. - начальная критическая нагрузка (по Н. П. Пузыревскому); g -
удельный вес грунта; d - глубина расположения слоя грунта, к которому прикладывается
нагрузка; с - сцепление грунта; φ - угол внутреннего трения грунта.
Развитие областей пластических деформаций осуществляется от угловых точек подошвы
фундамента и ориентировано вдоль осей (а), расположенных под углом Q = -j к вертикали
(рис. 1).
Вследствие этого в основании можно выделить 3 области: 1 - упругая область b1 ≤ Q
≤ p/2; 2 - пластическая область
b3 ≤ Q ≤
b1; 3 - упругая область -p/2
≤ Q ≤ b3.
Где b1 и b3
- углы раскрытия пластической области. При возрастании давления на основание пластическая
область будет увеличиваться, раскрываясь вправо и влево от первоначального направления
зарождения. Предельное развитие зон будет характеризоваться предельными значениями
углов bпр1 и
bпр3, определяемыми из выражения:
bпр1 =
p/4 - φ/2;
bпр3 = -p/4
- φ/2.
|
(2)
|
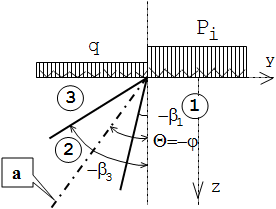
Рис. 1. Схема зарождения и развития пластической области в основании жёсткого фундамента
при плоской задаче: 1 и 3 – упругие области; 2 - пластическая область.